Konten [Tampil]
Pada materi Minggu lalu kita telah membahas tentang penyelesaian persamaan linear tiga variabel metode substitusi- eliminasi. Minggu ini kita akan mempelajari tentang persamaan linear tiga variabel dengan menggunakan Determinan.
Penyelesaian Persamaan Linear Tiga Variabel SPLTV metode Determinan
Contoh soal :
2x + y + z = 12
x + 2y - z = 3
3x - y + z = 11
Tentukan nilai x, y, z!
Jawab
Langkah pertama kita ubah persamaan diatas menjadi sebuah matriks 3 x 3
Langkah 1
Ambil koefisien yang di depan variabel x,y,z lalu susun menjadi tiga baris dan tiga kolom seperti berikut
Langkah 2
Ambil variabel, x , y, z susun dalam satu kolom. Lalu nilai persamaannya juga dibuat dalam satu kolom.
Langkah ke-3
Menentukan nilai Determinan D dengan cara menambahkan kolom 1 dan 2 ke sebelah kanan. Lalu buat tanda panah dengan arah diagonal ke kanan lalu dikurangkan dengan diagonal kiri.
Langkah-4
Menentukan Determinan x Dx caranya dengan mengganti kolom 1 dengan nilai persamaannya lalu lakukan seperti mencari nilai D tadi.
Setelah didapat nilai Dx lalu cari nilai x dengan cara membagi Dx /D
Langkah 5
Lakukan hal yang sama untuk menentukan nilai y. Tukar kolom ke-2 ganti dengan nilai persamaannya.
artikel lainnya : Soal dan Latihan SPLTV metode Determinan
Lakukan penyelesaian seperti cara pertama, kalikan nilai yang ada pada diagonal yang sama. Lalu kurangkan dengan nilai yang berlawanan arah diagonal ya.
Nilai y didapat dengan cara membagi Dy / D
Langkah 6
Untuk mencari nilai z langkah yang dilakukan sama halnya dengan ketika mencari nilai x dan y. Tukar kolom ke-3 menjadi nilai persamaan lalu kalikan ke arah diagonal yang sama.
Nilai x, y, dan z sudah didapatkan
X = Dx /D = -27/-9 = 3
Y = Dy / D. = -18/-9 = 2
Z = Dz / D. = 72/-9 = -8
Contoh 2
Selesaikan Persamaan linear tiga variabel berikut dengan metode determinan !
x + x - x = -3
x + 2 + 1 = 7
2 + 1 + 1 = 8
artikel terkait : Menyelesaikan Persamaan Trigonometri
Penyelesaian
Langkah 1
Ambil koefisien dari tiap tiap persamaan diatas sehingga menjadi matriks berordo 3 x 3
Langkah 2
Pindahkan kolom 1 dan 2 ke kanan. Sehingga matriks menjadi lebih luas. Lalu Operasinya setiap diagonalnya.
Langkah 3
Operasikan tiap tiap diagonal seperti arah tanda panah. Diagonal kanan di beri tanda positif + sedangkan diagonal kiri beri tanda negatif -
D = 1.2.1 + 1.1.2 + (-1.1.1) - 2.2.(-1 + 1.1.1 + 1.1.1)
D = 2 + 2-1 - -4 + 1+1
D = 3 - -2
D = 5
langkah 4
Pada langkah ke-4 kita akan menentukan nilai Dx dengan cara Tukar kolom pertama dengan nilai persamaan sehingga menjadi :
Selanjutnya pindahkan kolom pertama dan kedua ke sebelahnya sehingga matriks diperluas.
Selanjutnya kita akan mengoperasikan entri-entri yang ada di kolom-kolom diagonal seperti tanda panah pada gambar diatas.
Dx = (-3.2.1+1.1.8+ -1.7.1) - 8.2.(-1+1.1.-3+ 1.7.1)
Dx = -6 + 8 - 7 - -16 - 3 +7
Dx = -5 - -12
Dx = -5 + 12
Dx = 7
Sehingga X = Dx/D = 7/5
Langkah ke- 5
Selanjutnya kita akan menentukan Y dengan cara menukar kolom kedua dengan nilai persamaan nya. Seperti dibawah ini :
Lalu operasikan entri-entri pada diagonal diagonal matriks tersebut.
Lalu operasikan entri-entri seperti arah tanda panah.
Dy = 1.7.1 + (-3.1.2 + -1.1.8 ) - 2.7.(-1 + 8.1.1 + 1.1.-3
Dy = 7 -6 -8 - -14 + 8 -3
Dy = -7 - (-9
Dy = -7 + 9
Dy = 2
Langkah 6
Menentukan nilai Y = Dy/d = 2/5
Langkah 7
Langkah selanjutnya adalah menentukan Dz dengan cara menukar kolom ketiga dengan nilai persamaan. Seperti ditunjukkan dibawah ini :
Lalu operasikan entri-entri berdasarkan diagonal utama yang ada pada matriks yang telah kita perluas diatas.
Langkah 7
Selanjutnya kita akan mengoperasikan entri-entri seperti ditunjukkan tanda panah
Dz = 1.2.8 + 1.7.2 + (-3 .1.1 ) - 2.2.(-3 + 1.7. 1 + 8. 1.1)
Dz = 16 + 14 -3 - -12 + 7 + 8
Dz = 27 - 3
Dz = 24
Langkah 8
Menentukan nilai Z = Dz/D = 24/5
Himpunan penyelesaian yang telah kita dapatkan adalah 7/5, 2/5 ,24/5
Contoh 3
Selesaikan Persamaan Linear tiga variabel SPLTV berikut dengan metode Determinan!
x + y + 2z = 9
2x + 4y -3z = 1
3x + 6y - 5z = 0
Penyelesaian !
Untuk menyelesaikan SPLTV berikut kita ubah bentuk persamaan menjadi bentuk matriks
Langkah 1
Langkah 2
Selanjutnya kita akan menentukan nilai Determinan persamaannya sebagai berikut :
D = 1.4.(-5 + 1.-3.3+2.2.6 )- 2.4.3 + 1.(-3.3+1.2.-5)
D = -20-9+24-24-9-10
D = -5 - -4
D = -5+4
D = -1
langkah 3
Selanjutnya kita akan menentukan Determinan X dengan cara mengganti kolom pertama dengan nilai persamaannya.
Lalu kita perluas matriksnya dengan memindahkan entri pada kolom pertama dan kedua ke sebelahnya. sehingga matriks menjadi berikut ini :
Kalikan diagonal kanan lalu kurangkan dengan diagonal kiri
Dx= 9.4.(-5 + 1.-3.0 + 2.1.6) - 2.4.0 + 9.(-3.6+1.1.-5
Dx = -180 + 0 + 12 - 0 -162-5
Dx = -168 - -167
Dx = -1
Langkah 4
Selanjutnya kita akan menentukan Determinan Y dengan cara mengganti kolom kedua dengan nilai persamaannya.
Lalu kita perluas lagi matriksnya dengan memindahkan entri pada kolom pertama dan kedua ke sebelahnya sehingga matriks menjadi seperti berikut ini :
Kalikan diagonal kanan lalu kurangkan dengan perkalian diagonal kiri
Dy = 1.1.(-5 + 9.-3.3+2.2.0 ) - 2.1.3+ 1.(-3.0 + 9.2.-5)
Dy = -5-81+0-6+0-90
Dy = -86--84
Dy = -2
Langkah 5
Selanjutnya kita akan menentukan Determinan Z dengan cara mengganti kolom ketiga dengan nilai persamaannya.
Lalu kita perluas lagi matriksnya dengan memindahkan entri pada kolom pertama dan kedua ke sebelahnya sehingga matriks menjadi seperti berikut ini :
Selanjutnya kita operasikan entri entri pada diagonal-diagonal kanan dan dikurangi dengan entri-entri pada diagonal kiri.
Dz = 1.4.0+1.1.3+9.2.6-9.4.3+1.1.6+1.2.0
Dz = 0+3+108-108+6+0
Dz = 111 - 114
Dz = -3
Setelah kita mendapatkan nilai Dx, Dy dan Dz selanjutnya kita akan menentukan nilai x, y dan z dengan cara :
X = Dx/D = -1/-1 = 1
Y = Dy/D = -2 / -1 = 2
Z = Dz/D = -3 / -1 = 3
Sehingga himpunan penyelesaian dari persamaan linear tiga variabel soal
x + y + 2z = 9
2x + 4y -3z = 1
3x + 6y - 5z = 0
diatas adalah {1,2,3}
Contoh 4
Selesaikan Persamaan Linear Tiga Variabel berikut ini !
2x -3y + 3z = 3
x - y - 2z = -1
-x + 2y - 3z = -4
Penyelesaian :
Langkah 1 : Menentukan Determinan D
D =
D =
D = 2. (-1. -3 + -3. -2. -1) - 2. (-1. -1 + 2. -2. 2 + -3. 1. -3)
D = 6 - 6 + 4 - 2 - 8 + 9
D = 4 - 3
D = 1
Langkah 2 Menentukan Determinan y Dy
Tukar kolom pertama dengan nilai persamaannya
Dx =
Dx = 3.(-1. -3 + -3.-2.-4+2.(-1.2) - 2.-1.-4 + 3.-2.2 + -3.-1.-3)
Dx = 9 - 24 - 4 - 8 - 12 - 9
Dx = -9 - (-13)
Dx = -6
Langkah 3 Menentukan Determinan y Dy
Tukar kolom ke-2 dengan nilai persamaannya
Dy =
Dy = 2. (-1. -3 + -3. -2. -1 + 2.1. (-4 - 2. (-1. -1 + 2. -2. -4 + -3.1.-3)
Dy = 6 + 6 - 8 - 2 + 16 - 9
Dy = 4 - 9
Dy = -5
Langkah 4 Menentukan Determinan z Dz
Tukar kolom ke-3 dengan nilai persamaannya
Dz =
Dz = 2. (-1 .-4 + -3.-1.-1+ 3.1.-2) - 3.(-1.-1 + 2. -1.2 + -3.1.-4
Dz = 8 - 3 - 6 - 3 - 4 + 12
Dz = 11 - 11
Dz = 0
Dari hasil Determinan masing-masing variabel Dx. Dy, dan Dz kita akan menentukan nilai x, y, dan z dengan cara :
X = Dx/ D = -6 / 1 = 6
Y = Dy / D = -5 / 1 = -5
Z = Dz / D = 0 / 1 = 0
Sehingga himpunan penyelesaian untuk persamaaan Linear tiga variabel diatas adalah { -6, -5, 0}
Demikian Penyelesaian Persamaan Linear Tiga Variabel SPLTV metode Determinan. Untuk penyelesaian SPLTV bisa juga dilakukan dengan cara Substitusi eliminasi dan metode Gauss Jordan. Selamat mengikuti pembelajaran baik offline maupun online, di sekolah maupun di rumah atau di lembaga kursus. Semoga artikel ini membantumu.












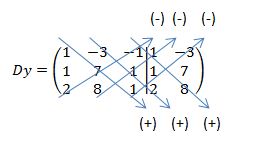













Maaf kak, untuk yang kakak kerjain kok pas nilai x, y, z saya input ke persamaan awal hasilnya jadi beda ya? Tks
ReplyDelete